[UNDER CONSTRUCTION...]
- Plasma turbulence
In astrophysical and space plasmas, a multitude of phenomena lead to the generation and release of free energy, that in turn drive the onset of turbulence. Such energy is usually injected at large (''fluid'') scales and then is nonlinearly transferred towards smaller and smaller scales trough that process known as turbulent cascade. Differently from what happens in neutral fluids, in plasmas the cascade of turbulent fluctuations is biased by the magnetic-field direction, and at fluid scales it constitutes the so-called magneto-hydrodynamic (MHD) inertial range. Following such a cascade, in a collisionless plasma the energy will eventually reach the characteristic microscopic (''kinetic'') length scales of the plasma (the Larmor radius and/or the inertial length), leading to the onset of non-MHD turbulent regimes. In this ''kinetic range'', both collisionless damping, dispersive effects of plasma modes and ''micro-instabilities'', can strongly affect the turbulent dynamics and the energy cascade. This is an intrinsically multi-dimensional, nonlinear problem: it would require to solve the Vlasov equation for the evolution of each species' distribution function f(x,v) in the six-dimensional phase space, (x,v), under the influences of electromagnetic forces, whose evolution are in turn determined, via Maxwell equations, by the distribution of sources which is encoded in f itself. A full-kinetic approach with realistic parameters is still computationally untreatable due to the huge separation of spatial and time scales. However, in most of the cases of interest, one can actually exploit such separation of scales and adopt the so-called ``reduced-kinetic'' models. In such models, one practically neglects a certain class of plasma processes: this is the case of, e.g., gyrokinetic (GK) and hybrid-kinetic (HK) models.
A few more details for an interested reader. Gyrokinetics: By assuming that the gyration of the charged particles around the magnetic field is a process much faster than any dynamic evolution due to the turbulent fluctuations, GK reduces the velocity space accessible to particles from “3V”, (v||, v⟂, θ), to a “2V” domain, (v||, v⟂) (here || and ⟂ are with respect to B0, θ is the gyroangle). Physically, this corresponds to a reduction from the actual (fast) helicoidal motion of charged particles along magnetic-field lines, where particles could “abruptly jump” from one field line to another, to the description of “charged rings of current” moving along those lines and only slowly drifting perpendicular to them. GK does not include cyclotron resonances and stochastic heating, but retains Landau damping of both species. Hybrid-kinetics: The HK description makes no approximations on the ions, i.e., the Vlasov equation is solved for the ion distribution function in a complete 6D phase space, whereas electrons are treated as a neutralising fluid. HK models include Landau damping, cyclotron resonances and stochastic heating for ions, but the electron kinetic effects are neglected (this approximation can be partially relaxed also within a hybrid-kinetic model; see, e.g., Finelli et al., A&A 2021)
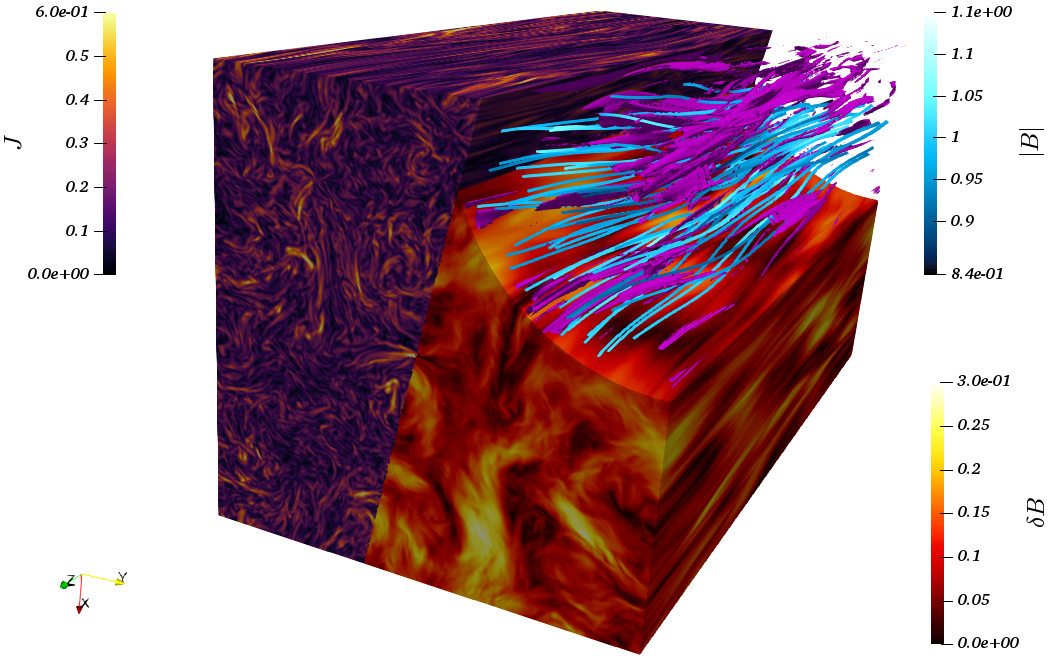
Figure. Three-dimensional rendering of current density, J, and magnetic-field fluctuations, δB.
Magnetic field lines with color-coded magnetic-field strength, |B|, are also shown, along with
embedded current density iso-surfaces (purple). The dataset used to produce this image is from
the "six-dimensional" (3D-3V: three-dimensional in both real and velocity spaces) simualtion
of kinetic turbulence at β=1 performed with the hybrid-Vlasov-Maxwell (HVM) code.
[ see Cerri et al., ApJL 846:L18 (2017) and Cerri et al., ApJL 856:L13 (2018) ]
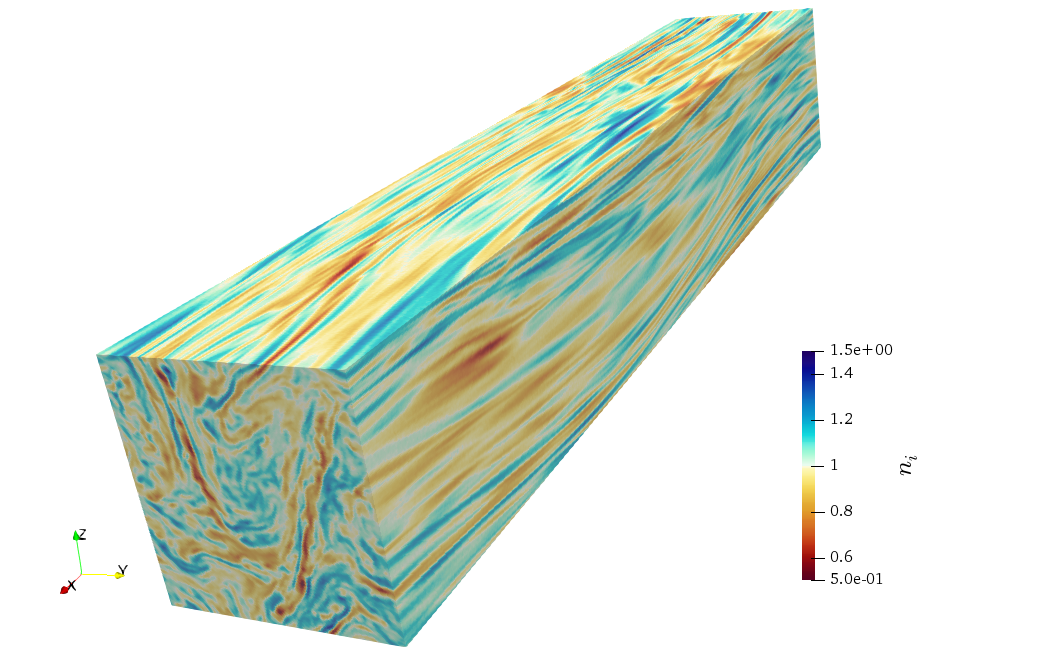
Figure. Three-dimensional rendering of ion density, ni, in a quasi-steady turbulent state.
The dataset used to produce this image is from a three-dimensional simualtion of continuously driven
kinetic turbulence at β ~ 0.1 performed with the hybrid particle-in-cell (PIC) code Pegasus++.
[ see Cerri et al., ApJ 916:121 (2021) ]
- Cosmic-ray transport in the Galaxy
The propagation of cosmic rays (CRs) through the turbulent interstellar medium (ISM) of our Galaxy is generally described in terms of the quasi-linear theory (QLT) of pitch-angle scattering on MHD waves, which is known to be strongly anisotropic with respect to magnetic-field direction and very sensitive to the properties of underlying turbulent fluctuations. However, the astro-particle community usually adopts a simplified phenomenological picture featuring just resonant pitch-angle scattering on Alfvén-wave packets and a constant, homogeneous diffusion coefficient, D0, throughout the Galaxy. This coefficient has been shown to have a power-law scaling with momentum-to-charge ratio (“rigidity”) p/Z, i.e., D0 ~ (p/Z)δ, and this parameter δ leaves a fingerprint in the propagated CRs spectra that are observed at the Earth. This simplified approach dates back to the early 60s, and was considered adequate to reproduce the available experimental data for a long time. However, such naive picture and its predictions have been seriously challenged both by theoretical arguments and by recent (direct and indirect) high-precision measurements. Beyond QLT, other plasma effects arising from CR–turbulence interaction itself play a relevant role within a self-consistent picture. Deriving accurate and self-consistent CR-propagation models in turbulent plasmas represent a great theoretical and numerical challenge, as it should relate the kinetic scales of CRs to the scale of the Galaxy itself (e.g., from ~ 10-6 to ~ 104 pc, respectively).
A few details for an interested reader. QLT theory, which is valid if the amplitude of the turbulent magnetic-field fluctuations δB is much smaller than the background field B0 (i.e., δB2/B02 << 1), formally predicts a highly anisotropic transport regime, where the ratio between the perpendicular and parallel diffusion coefficient is D⟂/D|| ~ F(k) ~ δBk2/B02 << 1 (here || and ⟂ are with respect to B0, and F(k) is the normalised power of the turbulent fluctuations δBk with wave vector k ~ 1/p, i.e. resonant with particles carrying momentum p). For instance, ISM turbulence is (mainly) injected by supernovae at scales LSN ~ 100 pc (and so one can assume δB/B0 ~ 1 at those scales). CR diffusion is provided by resonant scattering at the scale of the particle Larmor radius, rL: for typical galactic-CR energies, i.e., in the GeV–PeV range, their gyroradius is much smaller than the injection scales, rL << LSN (e.g., in a magnetic field of a few micro-Gauss, the Larmor radius of a CR with 1 GeV roughly corresponds to an astronomical unit, rL[1GeV] ~ 1013 cm ≈ 5 × 10-6 pc, i.e., (rL/LSN)1GeV ~ 10-7-10-8; and even at ~ 100 TeV, this ratio is just (rL/LSN)100TeV ~ 10-2-10-3). At those small scales (with respect to the injection scale) the turbulent power is extremely suppressed with respect to the injected one, so QLT is expected to hold. - Wind-magnetosphere interaction
Let us consider the Sun–Earth case. As soon as the supersonic, super-Alfv nic solarwind (SW) encounters the Earth, a magnetised shock (the “bow shock”), forms at the sunward boundaryof the Earth’s magnetopause. The shocked SW plasma forms the so-called “magnetosheath” and meets the Earth’s magnetosphere (MS). During mainly northward interplanetary magnetic field (IMF)conditions, no magnetic reconnection between the IMF carried by the solar wind and the Earth’s magneticfield could occur at the sunward MS boundaries. Therefore, accordingly to MHD theory, these two plasmas would not mix, and the shocked SW plasma just flows around the Earth’s magnetosphere. However, the velocity shear between such flowing SW and the stagnating MS plasma drives the Kelvin-Helmholtz instability (KHI) and the consequent formation of a (turbulent) mixing layer along the MS flanks, also due to secondary reconnetion and other non-ideal, kinetic instabilities (e.g., driven by pressure anisotropy and/or particle beams). This scenario provides an efficient mechanism for the entry of SW plasma and energetic particles into the MS. In general, depending on a planet’s magnetic field, wind–magnetosphere interaction determines the magnetospheric dynamics and, possibly, atmospheric loss. Thus, KHI, turbulence and other non-ideal plasma micro-instabilities (i.e., beyond the simple MHD description) play a crucial role in the coupling and transport between a stellar wind and a planet’s magnetosphere.





